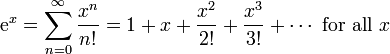Подтвердить что ты не робот

Эффективный способ вычисления математической константы e

Стандартное представление константы e как суммы бесконечного ряда очень малоэффективно для вычислений из-за многих операций деления. Итак, есть ли альтернативные способы эффективного вычисления константы?

Спасибо!

ИЗМЕНИТЬ

После выполнения некоторых из ваших ссылок я считаю, что эффективность исходит из метода, называемого бинарным расщеплением (в то время как представление все еще упоминается в серии), с которым я не знаком. Если кто-то знаком с этим, не стесняйтесь вносить свой вклад.

4b9b3361

ОТВЕТЫ

Ответ 1

Поскольку невозможно подсчитать каждую цифру "e", вам нужно будет выбрать точку остановки.

двойная точность: 16 десятичных цифр

В практических приложениях "максимально допустимое значение" с плавающей запятой "с двойной точностью, равным максимально возможному, до истинного значения" e "- приблизительно 16 десятичных цифр".

Как сказал KennyTM, это значение уже было предварительно рассчитано для вас в математической библиотеке. Если вы хотите рассчитать его сами, как указал Ханс Пассант, факториал уже растет очень быстро. Первые 22 члена в серии уже перегружены для вычисления этой точности - добавление дополнительных терминов из серии не изменит результат, если он хранится в 64-битной переменной с плавающей запятой с двойной точностью. Я думаю, вам потребуется больше времени, чтобы мигать, чем для вашего компьютера, чтобы сделать 22 деления. Поэтому я не вижу никаких причин для оптимизации этого.

тысячи, миллионы или миллиарды десятичных цифр

Как отметил Маттиу М., это значение уже было рассчитано, и вы можете загрузить его с веб-сайта Yee.

Если вы хотите рассчитать его сами, то многие цифры не будут соответствовать стандарту с плавающей запятой с двойной точностью. Вам нужна библиотека "bignum". Как всегда, вы можете использовать одну из многочисленных бесплатных библиотек bignum, которые уже есть, или изобретать колесо, создав свою собственную еще одну библиотеку bignum со своими особыми причудами.

Результат - длинный файл цифр - не очень полезен, но программы для его вычисления иногда используются в качестве эталонных тестов для проверки производительности и точности программного обеспечения библиотеки "bignum" и в качестве стресс-тестов для проверки стабильности и холодопроизводительность нового машинного оборудования.

Одна страница очень кратко описывает алгоритмы, которые Yee использует для вычисления математических констант.

Википедия "двоичное разбиение" статьи идет гораздо более подробно. Я думаю, что часть, которую вы ищете, представляет собой числовое представление: вместо внутреннего хранения всех чисел в виде длинной серии цифр до и после десятичной точки (или двоичной точки) Yee хранит каждый термин и каждую частичную сумму как рациональное число - как два целых числа, каждый из которых представляет собой длинную строку цифр. Например, скажем, одному из рабочих процессоров была назначена частичная сумма,

... 1/4! + 1/5! + 1/6! + ... .

Вместо того, чтобы делать деление сначала для каждого слагаемого, а затем добавлять, а затем возвращать единый миллионный результат с фиксированной точкой в ​​CPU менеджера:

// extended to a million digits
1/24 + 1/120 + 1/720 => 0.0416666 + 0.0083333 + 0.00138888

что ЦП может сначала добавить все члены серии вместе с рациональной арифметикой и вернуть рациональный результат в процессор-менеджер: два целых числа, возможно, несколько сотен цифр:

// faster
1/24 + 1/120 + 1/720 => 1/24 + 840/86400 => 106560/2073600

После того, как тысячи терминов были добавлены вместе таким образом, центральный процессор выполняет одно и то же разделение в самом конце, чтобы получить десятичные цифры после десятичной точки.

Не забывайте избегать PrematureOptimization и всегда ProfileBeforeOptimizing.

Ответ 2

Я не знаю никаких "более быстрых" вычислений, чем разложение Тейлора ряда, т.е.

e = 1/0! + 1/1! + 1/2! +...

или

1/e = 1/0! - 1/1! + 1/2! - 1/3! +...

Учитывая, что они были использованы А. Йи, который вычислил первые 500 миллиардов цифр e, я думаю, что там не так много оптимизировать (или лучше, его можно было бы оптимизировать, но никто еще не нашел пути, AFAIK)

ИЗМЕНИТЬ

Очень грубая реализация

#include <iostream>
#include <iomanip>

using namespace std;

double gete(int nsteps)
{
  // Let skip the first two terms
  double res = 2.0;
  double fact = 1;

  for (int i=2; i<nsteps; i++)
  {
    fact *= i;
    res += 1/fact;
  }

  return res;
}

int main()
{
  cout << setprecision(50) << gete(10) << endl;
  cout << setprecision(50) << gete(50) << endl;
}

Выходы

2.71828152557319224769116772222332656383514404296875
2.71828182845904553488480814849026501178741455078125

Ответ 3

Если вы используете double или float, в math.h уже существует константа M_E.

#define M_E         2.71828182845904523536028747135266250   /* e */

Существуют другие представления e в http://en.wikipedia.org/wiki/Representations_of_e#As_an_infinite_series; все они будут включать деление.

Ответ 4

Эта страница имеет хорошее изложение различных методов расчета.

Это небольшая программа C от Xavier Gourdon, чтобы вычислить 9000 десятичных цифр e на вашем компьютере. Аналогичная программа существует для π и для некоторых других констант, определяемых средними гипергеометрическими рядами.

[версия с дегустацией от https://codereview.stackexchange.com/a/33019]

#include <stdio.h>
int main() {
      int N = 9009, a[9009], x;
      for (int n = N - 1; n > 0; --n) {
          a[n] = 1;
      }
      a[1] = 2;
      while (N > 9) {
          int n = N--;
          while (--n) {
              a[n] = x % n;
              x = 10 * a[n-1] + x/n;
          }
          printf("%d", x);
      }
      return 0;
  }

Эта программа [при кодировании по коду] имеет 117 символов. Его можно изменить, чтобы вычислить больше цифр (измените значение 9009 на большее) и быстрее (измените константу 10 на другую мощность 10 и команду printf). Не так очевидный вопрос - найти используемый алгоритм.

Ответ 5

Я дал этот ответ в CodeReviews по вопросу относительно вычисления e по его определению через серии Тейлора (так что другие методы не были вариантом). В комментариях было предложено перекрестное сообщение. Я удалил свои замечания, относящиеся к этой другой теме; Те, кто заинтересован в дальнейших объяснениях migth, хотят проверить исходный пост.

Решение в C (должно быть достаточно легко адаптироваться к адаптации к С++):

#include <stdio.h>
#include <math.h>

int main ()
{
    long double n = 0, f = 1;
    int i;
    for (i = 28; i >= 1; i--) {
        f *= i;  // f = 28*27*...*i = 28! / (i-1)!
        n += f;  // n = 28 + 28*27 + ... + 28! / (i-1)!
    }  // n = 28! * (1/0! + 1/1! + ... + 1/28!), f = 28!
    n /= f;
    printf("%.64llf\n", n);
    printf("%.64llf\n", expl(1));
    printf("%llg\n", n - expl(1));
    printf("%d\n", n == expl(1));
}

Вывод:

2.7182818284590452354281681079939403389289509505033493041992187500
2.7182818284590452354281681079939403389289509505033493041992187500
0
1

Есть два важных момента:

  • Этот код не вычисляет 1, 1 * 2, 1 * 2 * 3,... который является O (n ^ 2), но вычисляет 1 * 2 * 3 *... за один проход (это O (n)).

  • Он начинается с меньших чисел. Если мы попытались вычислить

    1/1 + 1/2 + 1/6 +... + 1/20!

    и попытался добавить его 1/21!, мы добавили бы

    1/21!= 1/51090942171709440000 = 2E-20,

    до 2.что-то, что не влияет на результат (double содержит около 16 значащих цифр). Этот эффект называется underflow.

    Однако, когда мы начинаем с этих чисел, т.е., если мы вычисляем 1/32! +1/31! +... все они имеют некоторое влияние.

Это решение похоже на то, что C вычисляет с его функцией expl, на моей 64-битной машине, скомпилированной с gcc 4.7.2 20120921.

Ответ 6

Вы можете получить некоторую эффективность. Поскольку каждый член включает следующий факториал, некоторую эффективность можно получить, вспомнив последнее значение факториала.

e = 1 + 1/1! + 1/2! + 1/3! ...

Разлагая уравнение:

e = 1 + 1/(1 * 1) + 1/(1 * 1 * 2) + 1/(1 * 2 * 3) ...

Вместо вычисления каждого факториала знаменатель умножается на следующее приращение. Поэтому сохранение знаменателя в качестве переменной и умножение на него приведет к некоторой оптимизации.

Ответ 7

Если вы в порядке с приближением до семи цифр, используйте

3-sqrt(5/63)
2.7182819

Если вы хотите точное значение:

e = (-1)^(1/(j*pi))

где j - мнимая единица, а pi - известная математическая константа (Euler Identity)

Ответ 8

Метод двоичного расщепления хорошо поддается матричной метапрограмме, которая создает тип, представляющий рациональное, соответствующее аппроксимации e. 13 итераций, по-видимому, являются максимальными - любое превышение приведет к ошибке "интегрального постоянного переполнения".

#include <iostream>
#include <iomanip>

template<int NUMER = 0, int DENOM = 1>
struct Rational
{
    enum {NUMERATOR = NUMER};
    enum {DENOMINATOR = DENOM};

    static double value;
};

template<int NUMER, int DENOM>
double Rational<NUMER, DENOM>::value = static_cast<double> (NUMER) / DENOM;

template<int ITERS, class APPROX = Rational<2, 1>, int I = 2>
struct CalcE
{
    typedef Rational<APPROX::NUMERATOR * I + 1, APPROX::DENOMINATOR * I> NewApprox;
    typedef typename CalcE<ITERS, NewApprox, I + 1>::Result Result;
};

template<int ITERS, class APPROX>
struct CalcE<ITERS, APPROX, ITERS>
{
    typedef APPROX Result;
};

int test (int argc, char* argv[])
{
    std::cout << std::setprecision (9);

    // ExpType is the type containing our approximation to e.
    typedef CalcE<13>::Result ExpType;

    // Call result() to produce the double value.
    std::cout << "e ~ " << ExpType::value << std::endl;

    return 0;
}

Другой (не метапрограммный) шаблонный вариант во время компиляции рассчитает двойное приближение e. Этот номер не имеет ограничения на количество итераций.

#include <iostream>
#include <iomanip>

template<int ITERS, long long NUMERATOR = 2, long long DENOMINATOR = 1, int I = 2>
struct CalcE
{
    static double result ()
    {
        return CalcE<ITERS, NUMERATOR * I + 1, DENOMINATOR * I, I + 1>::result ();
    }
};

template<int ITERS, long long NUMERATOR, long long DENOMINATOR>
struct CalcE<ITERS, NUMERATOR, DENOMINATOR, ITERS>
{
    static double result ()
    {
        return (double)NUMERATOR / DENOMINATOR;
    }
};

int main (int argc, char* argv[])
{
    std::cout << std::setprecision (16);

    std::cout << "e ~ " <<  CalcE<16>::result () << std::endl;

    return 0;
}

В оптимизированной сборке выражение CalcE<16>::result () будет заменено фактическим двойным значением.

Оба варианта являются довольно эффективными, поскольку они вычисляют e во время компиляции: -)

Ответ 9

С моей точки зрения, наиболее эффективным способом вычисления e до желаемой точности является использование следующего представления:

e := lim (n -> inf): (1 + (1/n))^n

Особенно, если вы выберете n = 2^x, вы можете вычислить потенцию только с помощью умножения x, так как:

a^n = (a^2)^(n/2), if n % 2 = 0

Ответ 10

Существует несколько алгоритмов "пайки", которые вычисляют цифры последовательно неограниченным образом. Это полезно, потому что вы можете просто вычислить "следующую" цифру с помощью постоянного количества основных арифметических операций, не определяя заранее, сколько цифр вы хотите создать.

Они применяют серию последовательных преобразований, так что следующая цифра приходит к 1 месту, так что на них не влияют ошибки округления округления. Эффективность высока, потому что эти преобразования могут быть сформулированы как матричные умножения, которые сводятся к целочисленному сложениям и умножению.

Короче говоря, разложение в ряд Тейлора

e = 1/0! + 1/1! + 1/2! + 1/3! ... + 1/n!

Можно переписать, разлагая дробные части факториалов (заметим, что для регулярного перемещения рядов мы перемещаем 1 влево):

(e - 1) = 1 + (1/2)*(1 + (1/3)*(1 + (1/4)...))

Мы можем определить ряд функций f1 (x)... fn (x), таким образом:

f1(x) = 1 + (1/2)x
f2(x) = 1 + (1/3)x
f3(x) = 1 + (1/4)x
...

Значение e определяется из состава всех этих функций:

(e-1) = f1(f2(f3(...fn(x))))

Мы можем заметить, что значение x в каждой функции определяется следующей функцией и что каждое из этих значений ограничено на диапазоне [1,2] - то есть для любой из этих функций значение x будет 1 <= x <= 2

Так как это так, мы можем установить нижнюю и верхнюю границу для e, используя значения 1 и 2 для x соответственно:

lower(e-1) = f1(1) = 1 + (1/2)*1 = 3/2 = 1.5
upper(e-1) = f1(2) = 1 + (1/2)*2 = 2

Мы можем повысить точность, составив функции, определенные выше, и когда цифра соответствует нижней и верхней границам, мы знаем, что наше вычисленное значение e точно соответствует этой цифре:

lower(e-1) = f1(f2(f3(1))) = 1 + (1/2)*(1 + (1/3)*(1 + (1/4)*1)) = 41/24 = 1.708333
upper(e-1) = f1(f2(f3(2))) = 1 + (1/2)*(1 + (1/3)*(1 + (1/4)*2)) = 7/4 = 1.75

Так как цифры 1 и 10 разрядов совпадают, можно сказать, что приближение (e-1) с точностью до 10-го числа равно 1.7. Когда первая цифра совпадает между верхней и нижней границами, мы вычитаем ее, а затем умножаем на 10 - таким образом соответствующая цифра всегда находится в 1 месте, где точность с плавающей запятой высока.

Реальная оптимизация исходит из техники в линейной алгебре описания линейной функции как матрицы преобразования. Составные функции сопоставляются с матричным умножением, поэтому все эти вложенные функции могут быть сведены к простому целочисленному умножению и добавлению. Процедура вычитания цифры и умножения на 10 также представляет собой линейное преобразование и, следовательно, также может быть выполнена с помощью матричного умножения.

Другое объяснение метода: http://www.hulver.com/scoop/story/2004/7/22/153549/352

Статья, описывающая алгоритм: http://www.cs.ox.ac.uk/people/jeremy.gibbons/publications/spigot.pdf

Быстрое введение в линейные преобразования посредством матричной арифметики: https://people.math.gatech.edu/~cain/notes/cal6.pdf

NB этот алгоритм использует преобразования Mobius, которые являются типом линейного преобразования, кратко описанного в работе Gibbons.

Ответ 11

Из wikipedia заменить x на 1

alt text