Сэмплирование равномерно случайным образом из n-мерного единичного симплекса - это фантастический способ сказать, что вы хотите, чтобы n случайных чисел такие, что
- все они неотрицательны,
- они суммируются с одним, а
- каждый возможный вектор из n неотрицательных чисел, сумма которых равна единице, одинаково вероятна.
В случае n = 2 вы хотите выборочно выбирать из отрезка линии x + y = 1 (т.е. y = 1-x), который находится в положительном квадранте. В случае n = 3 вы выбираете из треугольной части плоскости x + y + z = 1, которая находится в положительном октанте R3:
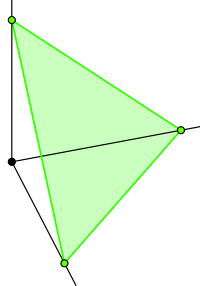
(Изображение из http://en.wikipedia.org/wiki/Simplex.)
Обратите внимание, что выбор n равномерных случайных чисел, а затем нормализация их, чтобы они суммировались с одним, не работает. Вы в конечном итоге со смещением к менее экстремальным числам.
Аналогичным образом, выбирая n-1 равномерные случайные числа, а затем занимая n-е число за один минус, сумма их также вводит смещение.
Википедия дает два алгоритма для этого: http://en.wikipedia.org/wiki/Simplex#Random_sampling (Хотя второй в настоящее время утверждает, что на практике это справедливо, но не теоретически. Я надеюсь, что это очистит или разъяснит, когда я это понимаю лучше. Я изначально застрял в "ПРЕДУПРЕЖДЕНИИ: такие-то бумажные заявления следующее неверно" на этой странице в Википедии, а кто-то другой превратил ее в "работает только на практике".)
Наконец, вопрос: Что вы считаете лучшей реализацией симплексной выборки в Mathematica (желательно с эмпирическим подтверждением ее правильности)?
Связанные вопросы