Как я могу суммировать следующую последовательность:
⌊n/1⌋ + ⌊n/2⌋ + ⌊n/3⌋ + ... + ⌊n/n⌋
Это просто O (n) решение на С++:
#include <iostream>
int main()
{
int n;
std::cin>>n;
unsigned long long res=0;
for (int i=1;i<=n;i++)
{
res+= n/i;
}
std::cout<<res<<std::endl;
return 0;
}
Вы знаете лучшее решение, чем это? Я имею в виду O (1) или O (log (n)). Спасибо за ваше время:) и решения
Изменить: Спасибо за все ваши ответы. Если кто-то хочет решение O (sqrt (n)): Python:
import math
def seq_sum(n):
sqrtn = int(math.sqrt(n))
return sum(n // k for k in range(1, sqrtn + 1)) * 2 - sqrtn ** 2
n = int(input())
print(seq_sum(n))
С++:
#include <iostream>
#include <cmath>
int main()
{
int n;
std::cin>>n;
int sqrtn = (int)(std::sqrt(n));
long long res2 = 0;
for (int i=1;i<=sqrtn;i++)
{
res2 +=2*(n/i);
}
res2 -= sqrtn*sqrtn;
std::cout<<res2<<std::endl;
return 0;
}
.
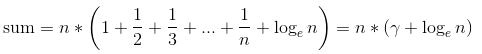
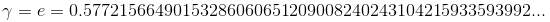
- трансцендентное число.)