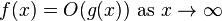Big-Oh: Как O (n) + O (n) +... + O (n) будет равно O (n ^ 2)?

Мне трудно понять следующие утверждения из Алгоритмы С. Дасгупты, C.H. Papadimitriou, и U.V. Vazirani - стр. 24), что они представляют сумму O (n) как O (n ²). Но мое понимание O (n) является линейной функцией от n, и оно никогда не может быть квадратичным независимо от того, сколько раз линейные функции добавлены (для любого заданного n). Они приводят объяснение, как показано ниже, для примера 13 x 11 в двоичной нотации.

        1 1 0 1
      x 1 0 1 1
      ----------
        1 1 0 1 (1101 times 1)
      1 1 0 1   (1101 times 1, shifted once)
    0 0 0 0     (1101 times 0, shifted twice)
+ 1 1 0 1       (1101 times 1, shifted thrice)
----------------
1 0 0 0 1 1 1 1 (binary 143)

Если x и y (1101 и 1011 здесь) являются как n битами, тогда представляют собой n промежуточных строк с длинами до 2n бит (принимая сдвиг в учетную запись). Общее время, затрачиваемое на добавьте эти строки, сделав два числа в момент времени O (n) + O (n) +... + O (n), которая является O (n ²), квадратичной в размер входов.

Извините, если это очевидно, но может кто-нибудь помочь мне понять, почему это O (n ²)?

Ответ 1

Если вы выполните что-то, что займет N секунд, и повторите это N раз. Сколько секунд потребуется, чтобы закончить?

N = 2 => 2*2 seconds.
N = 3 => 3*3 seconds.
N = 4 => 4*4 seconds.

      => N^2 seconds.

Ответ 2

Если существует n операций, которые имеют сложность O (n), то полная сложность равна n · O (n), которая является O (n ²).

Ответ 3

То, что является O (n), не является O (n ²) **, если оно умножается на постоянный коэффициент.

n is O(n)  
7n is O(n)  
100000n is O(n)

n*n is O(n^2)

Здесь формальное определение big-O, цитируемое из Википедии:

Пусть f (x) и g (x) - две функции определенных на некотором подмножестве вещественного номера. Один пишет

тогда и только тогда, когда при достаточно больших значения x, f (x) не превосходят a постоянная, умноженная на g (x) в абсолютная величина. То есть f (x) = O (g (x)) тогда и только тогда, когда существует положительное вещественное число M и реальное число x ₀ такое, что

** ПРЕДУПРЕЖДЕНИЕ: Big O - верхняя граница. Все, что O (n) также технически O (n ²). См. Big Theta и Big Omega для разграничения.

http://en.wikipedia.org/wiki/Big_O_notation

Ответ 4

Когда вы говорите "любое заданное n", вы забываете, что когда "данное n" является n, вы выполняете операцию O (n) n раз. Это n ².

Ответ 5

Если у вас есть операция O (n), и вы делаете это n раз, это определение O (n ^ 2).

Вы путаетесь с постоянным числом операций O (n), которое всегда равно O (n).

В примере двоичного умножения операция nmber из O (n) зависит от длины ввода, n.

Ответ 6

A O(n) сделанная операция n раз будет O(n^2). Более строго, если число операций O(n) линейно зависит от размера ввода, n, тогда у вас будет случай O(n^2).

Ответ 7

Многие ответы здесь забывают о важном предположении. Если у вас есть n операций, каждый из них O (n), то он не автоматически следует, что сумма равна O (n ²)! Скажем, k-я операция принимает k * n время (так что это постоянное время n) - первая операция занимает n, второе 2 * n и т.д. Тогда сумма первых n операций равна O (n ³).

Для неверующих, вот пример этого злоупотребления, из CLRS:

Ложное утверждение:

 n
 Σ  k = O(n)
i=1

Доказательство по индукции:

При n = 1, 1 = O (1).

При n + 1, если предположить, что для n выполнено предположение,

n+1       n
 Σ  k = ( Σ k) + (n+1) =  O(n) + n = O(n)
i=1      i=1

"Доказательство" неверно, сумма равна O (n ²).

Можно только сказать, что O (n) +... + O (n) есть O (n ²), если константы, скрытые в большом O , все ограничены некоторыми константа. В этом случае вы можете написать

O (n) +... + O (n) <= kn + kn +... + kn <= kn ²= O (n ²).

Если константы не ограничены, это неверно.

Ответ 8

Основная идея: поскольку постоянный множитель, спрятанный в O (n), будет увеличиваться с ростом n и поэтому будет не постоянным и создаст противоречие.

Одна из недостатков нотации Big-O заключается в том, что она поощряет ошибочные представления, подобные теме вашего вопроса. O (n) + O (n) предполагает, что вы добавляете к себе класс линейных функций, но на самом деле это означает "класс суммы любых двух линейных функций". Сумма снова линейна, что хорошо, но этот результат зависит от того, что существует только два (или любое постоянное число) суммируемых линейных функций.

Итак, в контексте ваш вопрос на самом деле означает "почему сумма возрастающих чисел линейных функций не является также линейной?". Эскиз доказательства довольно прост:

'
- Assume, for simplicity, that all linear functions are of the form f(n) = c*n, c >= 1
- Suppose we have an increasing-as-N-increases set of summed linear functions
- Assume the sum of that set of functions is linear, ie. of the form c*n
  - Try to find a value of c that works for all values of N
  - But, for any c that works for N=x, it will fail for N=x+1 because there is another addition
  - Contradiction
- The sum of the set of functions is not linear

Ответ 9

Вам нужно добавить два числа n-размера (с учетом времени O (n)), n раз. n (O (n)) = O (n * n) = O (n ^ 2).

Ответ 10

Ответ очень прост:

O (n) + O (n) + ··· + O (n) = X (n)

Если X является постоянным и не изменяется с вводом, то он все еще равен O (n).