Я реализую поведение прокрутки интерфейса пользовательского интерфейса с сенсорным экраном, но я слишком устал в этот момент, чтобы обдумать какую-то предположительно тривиальную часть математики:
y (distance/velocity)
|********
| ******
| ****
| ***
| ***
| **
| **
| *
| *
-------------------------------- x (time)
F (X) →
Пользовательский интерфейс должен позволять пользователю перетаскивать и "бросать" представление в любом направлении и удерживать его прокруткой некоторое время даже после того, как он отпустит палец с экрана. Это своего рода импульс, который зависит от того, насколько быстро пользователь тянул, прежде чем он снял палец.
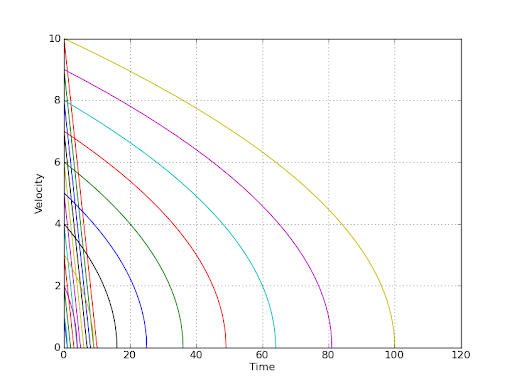
Итак, у меня есть начальная скорость (v0), и каждые 20 мс я прокручиваю на величину относительно текущей скорости. С каждой итерацией прокрутки я немного понижаю скорость до тех пор, пока она не опустится ниже порога, когда я остановлю ее. Это просто не выглядит правильным, когда я уменьшаю его на фиксированное количество (линейное), поэтому мне нужно моделировать отрицательное ускорение, но не придумать достойную простую формулу, как рассчитать количество, на которое я должен снизить скорость на каждой итерации.
Update:
Спасибо за ваши ответы, но до сих пор мне не удалось получить удовлетворительную функцию из отзывов. Я, вероятно, недостаточно описал желаемое решение, поэтому я попытаюсь привести пример реального мира, который должен показать, какой расчет я хотел бы сделать:
Предположим, что на определенной улице есть определенный автомобиль, и водитель нажимает на тормоза до максимума, пока автомобиль не остановится. Водитель делает это с одним и тем же автомобилем на одной и той же улице несколько раз, но начинает тормозить с разной скоростью. Пока машина замедляется, я хочу, чтобы она могла рассчитать скорость, она будет ровно на одну секунду позже, основываясь только на ее текущей скорости. Для этого расчета не должно иметь значения, с какой скоростью автомобиль ехал, когда водитель начал ломаться, так как все экологические факторы остаются неизменными. Конечно, в формуле будут какие-то константы, но когда автомобиль упадет до 30 м/с, он будет идти на одинаковое расстояние в следующую секунду, независимо от того, ехал ли он на скорости 100 или 50 м/с, когда водитель начал разрываться, Таким образом, время, прошедшее с момента разрыва, также не будет параметром функции. Торможение с определенной скоростью всегда будет одинаковым.
Как вы вычисляете скорость через секунду в такой ситуации, предполагая некоторые произвольные постоянные для замедления, массы, трения или чего-то еще и игнорируя усложняющие влияния, такие как сопротивление воздуха? Я только после кинетической энергии и ее диссипации из-за трения от взлома автомобиля.
Обновление 2 Теперь я вижу, что ускорение автомобиля будет линейным, и на самом деле это не то, что я искал. Я очищу это и завтра выберу новые предложения. Спасибо за ваш вклад.